△1日1回!押して応援おねがいします!△
ちょっとしたゲームの確率に意見が食い違い喧嘩をはじめたアオイとシオン・・・
はたしてどっちの意見が正しい?

絶対1/2だって!!!

いいえ!これらはまやかし!!1/3です!!

カスミさんはどっち?!

・・・


確率で言ったら、二人とも不正解なのです・・・

えええ?!

いったい、どういうこと?!

今日はこのお話をしましょうか。
モンティ・ホール問題

アメリカのテレビ番組で出題された際に議論を呼んだため、その司会者の名前がつけられた問題です。

3つの扉があり、1つはアタリ、2つはハズレです。
挑戦者は3つの中から1つの扉を選びます。
司会者は答えを知っており、挑戦者が選んだ扉以外の2つの中から不正解の扉を選んで開けます。
挑戦者は残り2つの扉から再度選ぶことが可能。
はたして、挑戦者は扉を選び直すべきかどうか?確率はどうなるか?といった問題。
この問題は多くの人が確率を誤って答えてしまう問題である。
ほとんどの人が、確率は1/3か1/2と答えてしまうが誤りである。
そしてこれは「確率の専門家」ですら間違えてしまうほどの問題として有名になった。

専門家ですら間違えるのですか・・・


それで、1/2でも1/3でもないなら正解はいくつなのさ!

これはですね、図で解説したほうがわかりやすいと思うので図で解説しますね。
Aをアタリの扉、BとCをハズレの扉とします。
まず、「選び直さない場合」と「選び直した場合」とで分けて考えます。
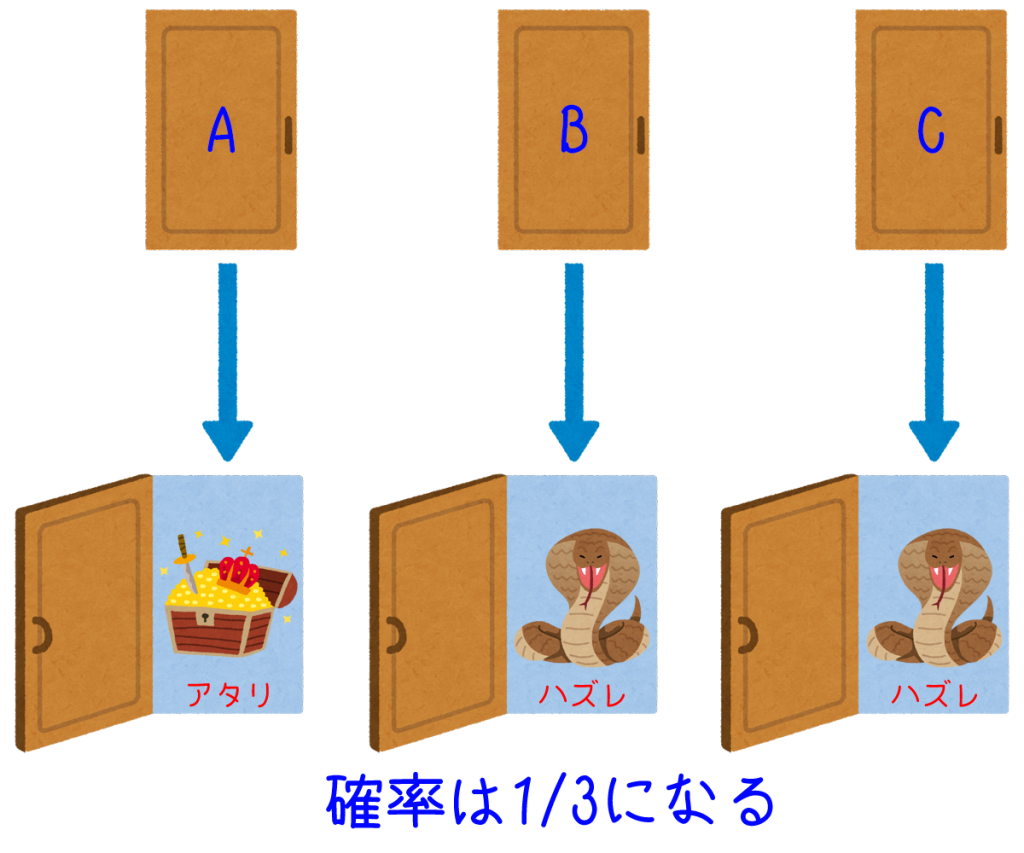
選び直さない場合は、パターンは1つしかなくそのまま確率は1/3となります。
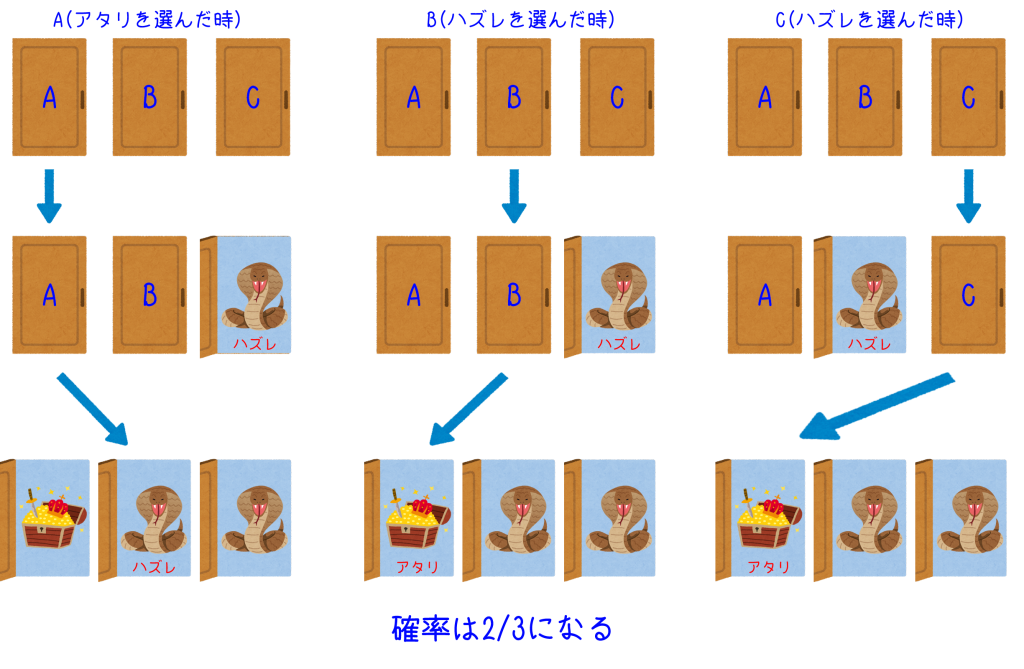
選び直した場合は、パターンが3つあります。
1.最初に選んだ扉がA(アタリ)のときは、選び直すことでハズレになってしまう。
(司会者がBとCどちらを開けても一緒)
2.最初に選んだ扉がB(ハズレ)のときは、司会者はC(ハズレ)を開けるはずなので、選び直すことでA(アタリ)にたどり着く。
3.最初に選んだ扉がC(ハズレ)のときは、司会者はB(ハズレ)を開けるはずなので、選び直すことでA(アタリ)にたどり着く。
選び直す場合この3パターンが存在し、そのうちアタリのパターンは2つあるため、確率は2/3まで上がる。
扉を選び直した時に、確率が反転するため(アタリだったらハズレ、ハズレだったらアタリに)あたる確率が1/3だったものが2/3になります。

正解を知っている司会者が手を出すという所がミソなんですよね♪
たったこれだけで確率が2/3まで上がってしまうのです。


たしかに・・・図で見ると納得できますが・・・
直感で考えると間違えますね・・・

そうだね;;
でも、面白そうだからフレンドで試してみようかな?

そうですね、なので頭脳派と個性派の揃うカスミルームでも試してみました。

おお!

次回、どんな珍回答がでるか?!
そしてこの確率の誤謬から私たちが気をつけなければいけない教訓についてお話させていただきたいと思います。
おしまい
▽お帰りはこちらから♪▽
△1日1回!押して応援おねがいします!△



